728x90
위상 정렬: 방향 그래프의 모든 노드를 '방향성에 거스르지 않도록 순서대로 나열하는 것
위상 정렬은 정렬 알고리즘의 일종입니다. 순서가 정해져 있는 일련의 작업을 차례대로 수행할 때 사용할 수 있는 알고리즘입니다. 또한, 시간 복잡도는 O(V+E)입니다.
1. 진입차수가 0인 노드를 큐에 넣습니다.
2. 큐가 빌 때까지 다음의 과정을 반복합니다.
2-1) 큐에서 원소를 꺼내 해당 노드에서 출발하는 간선을 그래프에서 제거합니다.
2-2) 새롭게 진입차수가 0이 된 노드를 큐에 넣습니다.



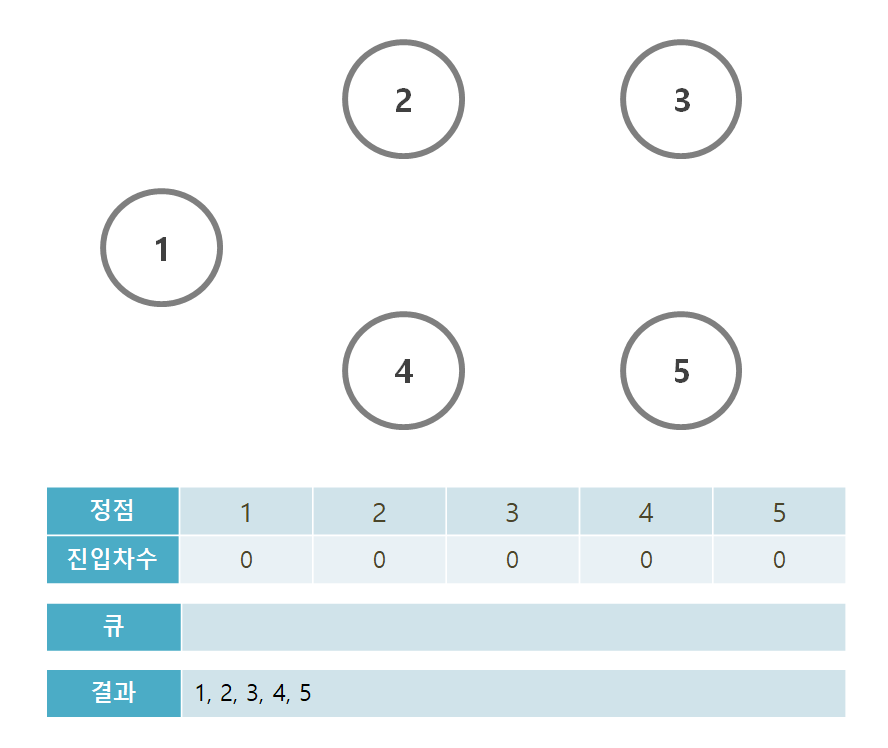
이처럼 진입차수가 0인 노드부터 실행합니다. 만약에 한 단계에서 큐에 새롭게 들어가는 원소가 2개 이상인 경우가 있다면, 답이 여러가지가 될 수 있다는 특징을 가집니다.
(3,4)의 간선이 없다면 1-2-4-3-5, 1-4-2-5-3이 답이 될 수 있습니다.
입력 예시)
7 8
1 2
1 5
2 3
2 6
3 4
4 7
5 6
6 4
출력 예시)
1 2 5 3 6 4 7
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
|
from collections import deque
#노드의 개수와 간선(union 연산)의 개수 입력받기
v, e = map(int, input().split())
#모든 노드에 대한 진입 차수는 0으로 초기화
indegree = [0] * (v+1)
#각 노드에 연결된 간선 정보를 담기 위한 연결 리스트(그래프) 초기화
graph = [[] for i in range(v+1)]
#방향 그래프의 모든 간선 정보를 입력받기
for _ in range(e):
a, b = map(int, input().split())
graph[a].append(b) #정점 A에서 B로 이동 가능
#진입차수를 1 증가
indegree[b] += 1
#위상 정렬 함수
def topology_sort():
result = [] #알고리즘 수행 결과를 담을 리스트
q = deque() #큐 기능을 위한 deque 라이브러리 사용
#처음 시작할 때는 진입차수가 0인 노드를 큐에 삽입
for i in range(1, v+1):
if indegree[i] == 0:
q.append(i)
#큐가 빌 때까지 반복
while q:
#큐에서 원소 꺼내기
now = q.popleft()
result.append(now)
#해당 원소와 연결된 노드들의 진입차수에서 1 빼기
for i in graph[now]:
indegree[i] -= 1
#새롭게 진입차수가 0이 되는 노드를 큐에 삽입
if indegree[i] == 0:
q.append(i)
#위상 정렬을 수행한 결과 출력
for i in result:
print(i,end = ' ')
topology_sort()
|
cs |
728x90
'코딩테스트 > 그래프이론' 카테고리의 다른 글
| <PART 2>그래프이론 예제 (0) | 2022.11.13 |
|---|---|
| <PART 2> 그래프이론 (크루스칼 알고리즘) (0) | 2022.11.12 |
| <PART 2>그래프이론 (서로소 집합) (0) | 2022.11.12 |


댓글